前回、次は「自然言語」と予告いたしましたが、これまでscikit-learnのライブラリを使っていたSVM(サポートベクターマシン)について、自分なりの理解で解説と、ライブラリを使わない実装に挑戦していきたいと思います!
scikit-learn を使ったSVMについては、以下の過去記事をご参照ください。
今回のお品書きは以下の通りです。
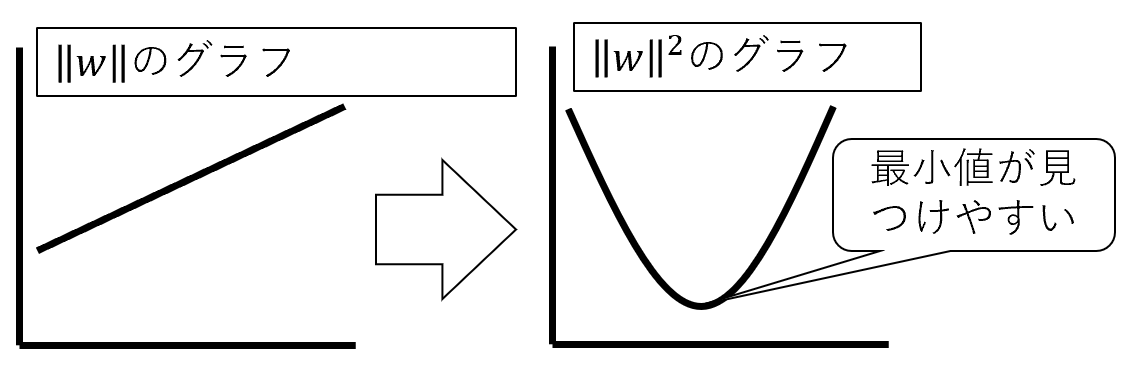
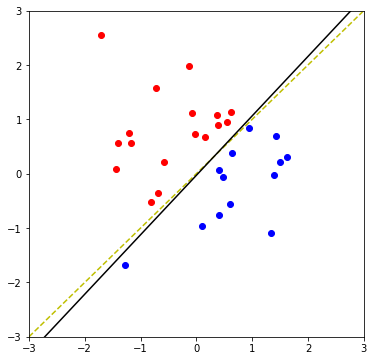
SVM(サポートベクターマシン)とは、教師あり学習のモデルの一つです。 回帰にも、分類にも使うことができます。(今回は、分類で解説いたします。) SVMの考え方は、2値分類の場合、以下の基準を満たす境界線(多次元の場合は境界となる超平面)を表す重みwと閾値bを見つけるということになります。 図で表すと以下の通りとなります。 この境界線を使って、新たなデータについて、境界線より上(w*X-b>0)の場合はクラスA、境界線より下(w*X-b<0)の場合は、クラスBと分類できるようになります。 まずは、SVMで分類するためのデータを作成します。 今回は、2つの特徴量をもつ、30個のランダムデータを作成します。 また、正解データとしては、特徴量1より特徴量2が大きければ「1」、小さければ「-1」 としました。 import numpy 作成したデータをプロットすると以下の通りです。 from matplotlib import pyplot pyplot.figure(figsize = (6, 6)) SVMの考え方の1点目の、クラスA、クラスBに関する基準につき、もう少し掘り下げて考えてみます。 各クラスのラベルデータ(正解データ)は以下の通りです。 また、クラスAのデータが境界線より上、クラスBが境界線より下となるので、重みwと閾値bは以下の条件を満たす必要があります。 クラスAのときは式1、式2ともに正、クラスBのときは式1、式2ともに負なので、SVMが満たすべき基準の1つ目は、以下を満たすことであると定義できます。 次に、SVMの二つ目の基準について考えてみます。 ある点x[i]から直線(w*x-b)までの距離dは、以下の式で表されます。(この式の導入については省略します。) ここで、分子に着目してみると、前述の式3のカッコ内の絶対値となっています。 式3では、T[i]を掛けることで常に正の数に変換していて、絶対値をとることと同義になっています。 よって、式4は以下に変換することができます。 マージンMは、境界線から最も近いX[i]になるので、すべてのX[i]からの距離(式5のd)は、必ずM以上となり、以下の式が成り立ちます。 これで、Mの上限を抑え込むことができました。 マージンMは、分子が最小になるときの値となるので、①Mが最大となるのは、分母の||w||が最小値をとるときになります。 ||w||は正の値なので、||w||が最小値となるときは、➁||w||の二乗も最小値となります。二乗にすることで、凸型の関数に変換できます。 ①、➁より、Mを最大にするということは、以下の通り||w||の2乗を最小とすることと等価となります。(定数をかけても最小となるwは変わらないので、今後の処理で必要となる微分を考慮して、2分の1をかけています。) 式6の両辺をMで割ると以下の式になります。 単純化するために、w,bを、それぞれ以下で置き換えます。 置き換えた結果が以下の式です。 これが、Mを最大にするw,bの制約条件になります。 以上より再整理すると、以下の通りの問題を解くことに帰着しました。 【問題】以下の関数を最小化するwを求める。 【条件】以下を制約条件とする。 4項で整理した問題を解くために、ラグランジュ未定定数法を使います。 今回は詳しく説明しませんが、4項で整理した問題のように、制約条件付きで最小値・最大値などの極値を求める問題を、単純な極値を求める問題に変換する方法になります。 具体的には、極値を求めたい目的関数f(x)を最小にする点をn個の不等式制約g(x)≧0のもとで、以下の通り求める。 この時、以下を解くことで、最小値、最大値になる主変数を求めることができます。 では、4項で整理した問題に、5項で確認したラグランジュ未定乗数法を適用します。 同様に主変数を求める式14の4つの式に当てはめます。 式15を展開して、式16の①w,①bを代入します。 これにより、ラグランジュ未定乗数αと訓練データX[i]とラベルデータT[i]の線形和で、制約条件付きの最小値を求める問題から、L(α)を最大化するαiを求める単純な問題に落とし込むことができました。 なかなかに、ハードな内容でしたが、やっとこれでw,bの解を求める準備が整いました。 L(α)の最大となるαを求めるために、最急降下法を使います。 最急降下法は、その時点でのαiで偏微分した際の微分値によってL(α)が最小値に向かう方向にαiを更新していく手法です。 以下のように更新していきます。 式17をαiで偏微分した式を代入すると以下の通りとなります。 この式をpythonで実装すると以下の通りになります。 alpha = numpy.zeros(N) #αの初期値 # 学習回数分繰り返す また、 この式をpythonで実装すると以下の通りとなります。 #αiが正かどうかをindexに格納 これまでの内容をpythonで実装すると以下のコードになります。 import numpy alpha = numpy.zeros(N) #αの初期値 # 学習回数分繰り返す #αiが正かどうかをindexに格納 #縦横6x6サイズに-3~3の範囲でグラフを描画 先ほどのコードを実行すると以下の結果が得られました。 黄色い破線が正解ラベルデータの境界線(特徴量1と特徴量2が同じになる線)で、黒い実線がSVMで学習した境界線になります。 データ数も30個で、学習回数も1000回程度でなかなか良い結果がえられたと思います。 今回は、SVMの解説に挑戦してみました。数式がたくさんで、すごく大変でした。 なるべく自分の理解で分かりやすくお伝えできるように頑張ったのですが、いかがでしたでしょうか。 お伝えしきれなかった部分は、参考書等でご確認いただければと思います。 これからもわかりやすいコンテンツ作りに精進してまいりたいと思います。 【過去記事】 2019年8月31日(土)にE資格を受験して、合格しました! E資格対策として勉強の進め方や、参考書などをまとめました。 これから受験される方がいらっしゃいましたらご参考まで。 2019年3月9日(土)にG検定を受験し、見事合格できました! 受験の体験記や勉強法などを別のブログにまとめました。 これから受験される方がいらっしゃいましたらご参考まで。 【E資格対策に使った参考書】 SVM(サポートベクターマシン)の解説
1.SVM(サポートベクターマシン)とは何か。

2.分類するデータを作成する。
numpy.random.seed(614)
N = 30 # データの個数
d = 2 # 特徴量の数(次元数)
# 30個x2次元の訓練データを作成する
X = numpy.random.randn(N, d)
# 30個の正解データを作成する
#(特徴量1より特徴量2が大きい場合 1,小さい場合 -1)
T = numpy.array([1 if feature1 < feature2 else - 1 for feature1, feature2 in X])
pyplot.xlim(-3, 3)
pyplot.ylim(-3, 3)
pyplot.plot(X[T == 1,0], X[T == 1,1], 'ro')
pyplot.plot(X[T == -1,0], X[T == -1,1], 'bo')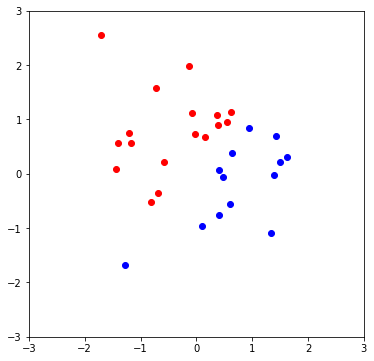
3.クラスA、クラスBについて考えてみる。
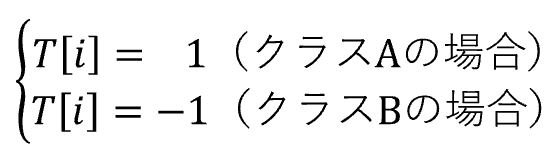
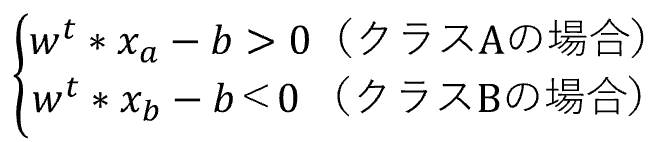
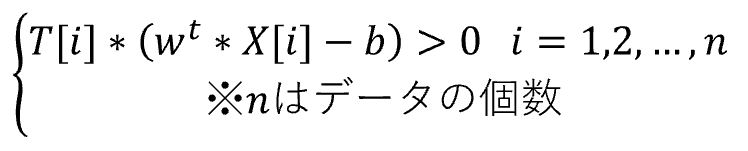
3.マージンの最大化について考えてみる。
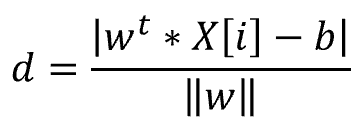
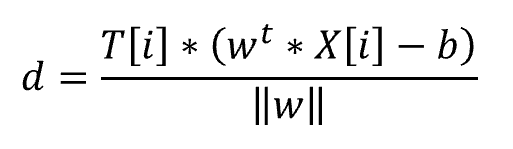
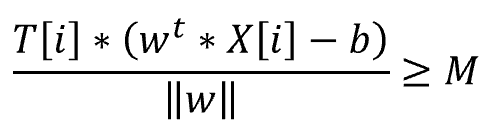
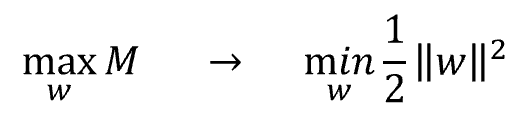
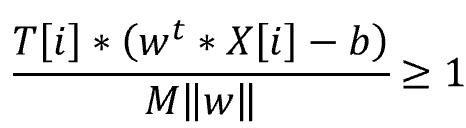
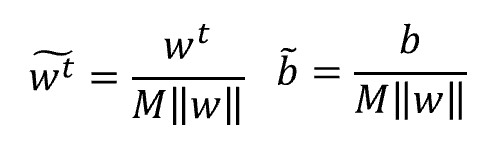
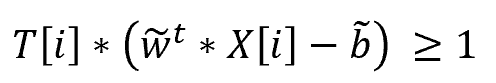
4.解く問題の再整理
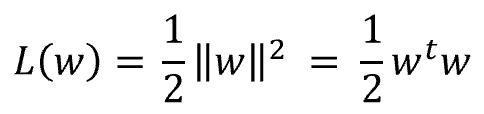
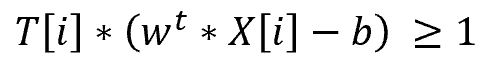
5.ラグランジュ未定乗数法について
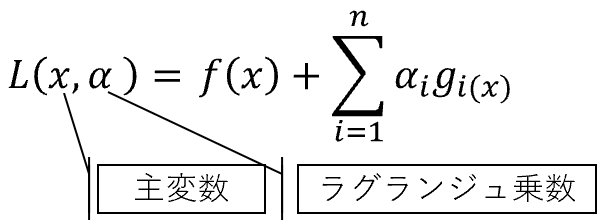

6.ラグランジュ未定乗数法を適用する。
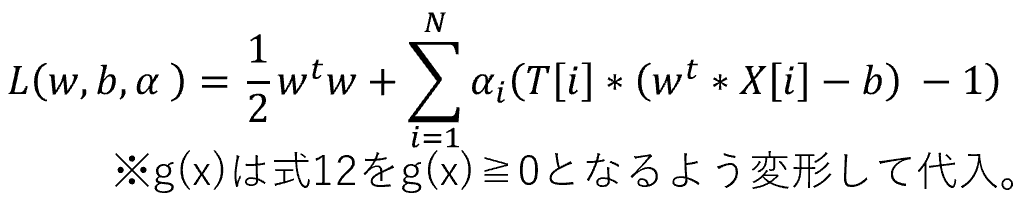
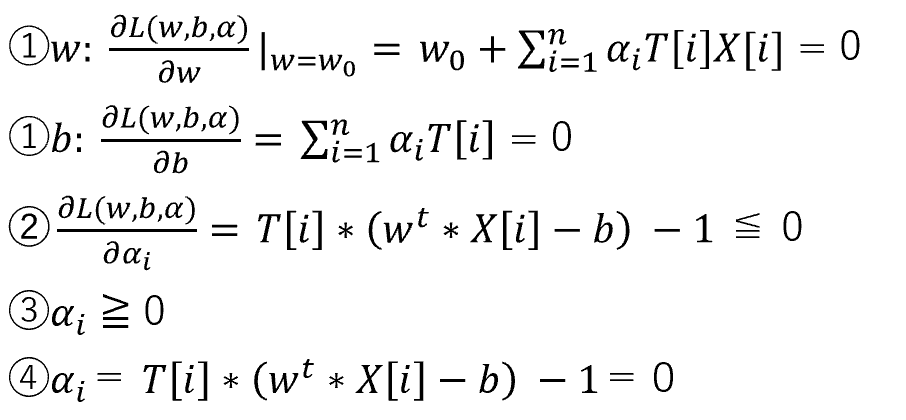
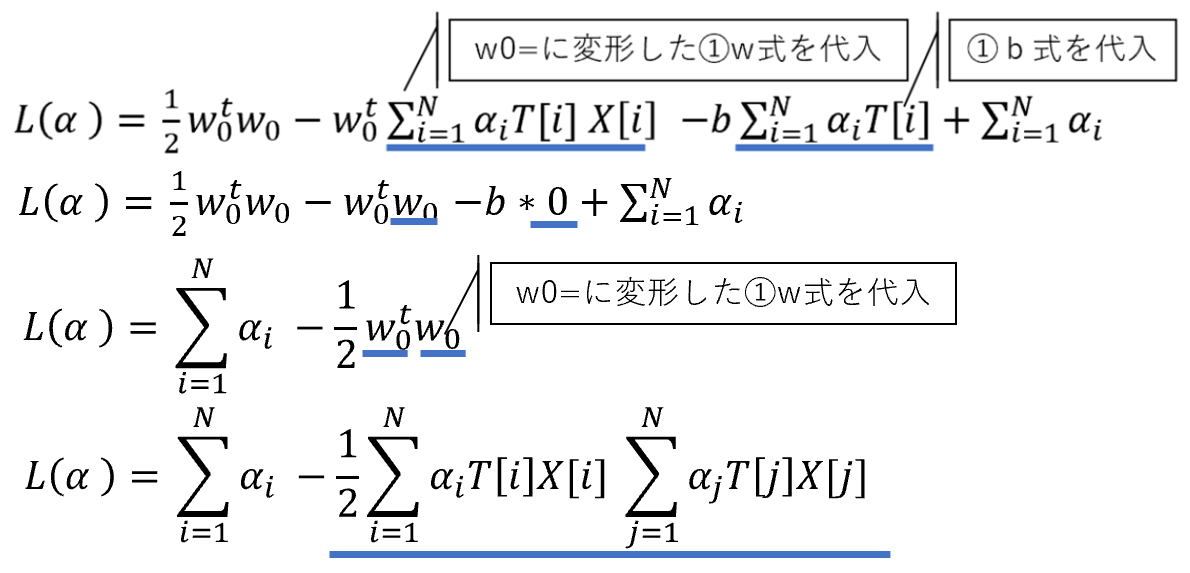
7.解を求める。
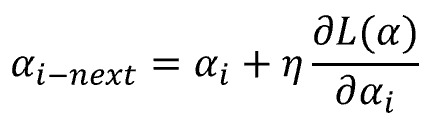
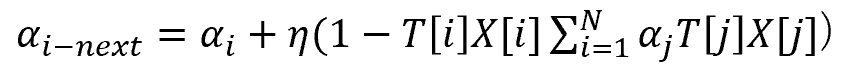
eta_al = 0.0001 # αの更新率(η)
itr = 1000 #学習回数
for _itr in range(itr):
# αiについてi=1からN(データ数30個)まで繰り返す
for i in range(N):
# 式23のカッコ内の計算を実施
delta = 1 - (T[i] * X[i]).dot(alpha * T * X.T).sum()
# 式23のαi-nextの計算を実施
alpha[i] += eta_al * delta![]() をL(α)を最大化するα、Ts、Xsをそれぞれ、マージンMが最小となるラベルデータ、訓練データとすると、求めるw,bは式16の①wの変形、および式16の④から以下の通りで求められます。
をL(α)を最大化するα、Ts、Xsをそれぞれ、マージンMが最小となるラベルデータ、訓練データとすると、求めるw,bは式16の①wの変形、および式16の④から以下の通りで求められます。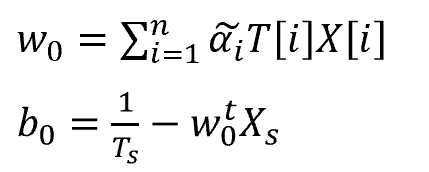
index = alpha > 0
#式20からw,bを求める
w = (alpha * T).T.dot(X)
b = (T[index] - X[index].dot(w)).mean()8.全体像
from matplotlib import pyplot
numpy.random.seed(614)
N = 30 # データの個数
d = 2 # 特徴量の数(次元数)
# 30個x2次元の訓練データを作成する
X = numpy.random.randn(N, d)
# 30個の正解データを作成する
#(特徴量1より特徴量2が大きい場合 1,小さい場合 -1)
T = numpy.array([1 if feature1 < feature2 else - 1 for feature1, feature2 in X])
eta_al = 0.0001 # αの更新率(η)
itr = 1000 #学習回数
for _itr in range(itr):
# αiについてi=1からN(データ数30個)まで繰り返す
for i in range(N):
# 式23のカッコ内の計算を実施
delta = 1 - (T[i] * X[i]).dot(alpha * T * X.T).sum()
# 式23のαi-nextの計算を実施
alpha[i] += eta_al * delta
index = alpha > 0
#式20からw,bを求める
w = (alpha * T).T.dot(X)
b = (T[index] - X[index].dot(w)).mean()
pyplot.figure(figsize = (6, 6))
pyplot.xlim(-3, 3)
pyplot.ylim(-3, 3)
#線を描画するためのサンプリング間隔を作成
seq = numpy.arange(-3, 3, 0.02)
#正解データの境界線を黄色の破線で表示
pyplot.plot(seq,seq,'y--')
#SVMで学習した境界線を黒の実線で表示
pyplot.plot(seq, -(w[0] * seq + b) / w[1], 'k-')
#正解ラベルが1のデータを赤点でプロット
pyplot.plot(X[T == 1,0], X[T == 1,1], 'ro')
#正解ラベルが-1のデータを青点でプロット
pyplot.plot(X[T == -1,0], X[T == -1,1], 'bo')
pyplot.show()9.実行してみる。
![[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。] [商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]](https://hbb.afl.rakuten.co.jp/hgb/0f083428.235a9254.0f083429.dafd0742/?me_id=1213310&item_id=19252992&m=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fbook%2Fcabinet%2F3965%2F9784797393965.jpg%3F_ex%3D80x80&pc=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fbook%2Fcabinet%2F3965%2F9784797393965.jpg%3F_ex%3D128x128&s=128x128&t=picttext)
![[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。] [商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]](https://hbb.afl.rakuten.co.jp/hgb/0f083428.235a9254.0f083429.dafd0742/?me_id=1213310&item_id=11357465&m=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fbook%2Fcabinet%2F3201%2F32012134.jpg%3F_ex%3D80x80&pc=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fbook%2Fcabinet%2F3201%2F32012134.jpg%3F_ex%3D128x128&s=128x128&t=picttext)